[백준] Baekjoon Online Judge
문제
대구 달성공원에 놀러 온 지수는 최근에 새로 만든 타일 장식물을 보게 되었다. 타일 장식물은 정사각형 타일을 붙여 만든 형태였는데, 한 변이 1인 정사각형 타일부터 시작하여 마치 앵무조개의 나선 모양처럼 점점 큰 타일을 붙인 형태였다. 타일 장식물의 일부를 그리면 다음과 같다.
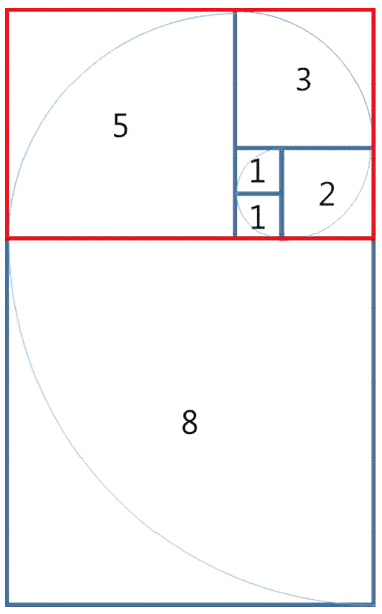
그림에서 타일에 적힌 수는 각 타일의 한 변의 길이를 나타낸다. 타일 장식물을 구성하는 정사각형 타일 한 변의 길이를 안쪽 타일부터 시작하여 차례로 적으면 다음과 같다.
1, 1, 2, 3, 5, 8, ...
지수는 문득 이러한 타일들로 구성되는 큰 직사각형의 둘레가 궁금해졌다. 예를 들어, 처음 다섯개의 타일이 구성하는 직사각형(위에서 빨간색으로 표시한 직사각형)의 둘레는 26이다.
타일의 개수 N(1 ≤ N ≤ 80)이 주어졌을 때, N개의 타일로 구성된 직사각형의 둘레를 구하는 프로그램을 작성하시오.
입력
표준 입력으로 다음 정보가 주어진다. 입력은 한 줄로 구성되며 이 줄에는 타일의 개수를 나타내는 정수 N(1 ≤ N ≤ 80)이 주어진다.
출력
표준 출력으로 N 개의 타일이 구성하는 타일 장식물 직사각형의 둘레를 출력한다.
64비트 정수형인 “long long” 자료형을 써야할 수 있음
풀이
#include <iostream>
using namespace std;
long long arr[81];
void init(int N);
void init(int N) {
arr[0] = arr[1] = 1;
for (int i = 2; i < N; i++)
arr[i] = arr[i - 1] + arr[i - 2];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int N;
cin >> N;
init(N);
cout << arr[N - 1] * 4 + arr[N - 2] * 2 << '\n';
return 0;
}피보나치 수열을 N만큼 구한 뒤에 이를 사용해서 직사각형의 둘레를 구하면 된다.
직사각형의 둘레는 (가장 큰 타일 * 4 + 다음으로 큰 타일 * 2)와 같다.
'백준 > C++' 카테고리의 다른 글
| [Baekjoon/C++] 25631번 - 마트료시카 합치기 (0) | 2025.09.15 |
|---|---|
| [Baekjoon/C++] 15687번 - 직사각형 (0) | 2025.09.14 |
| [Baekjoon/C++] 25644번 - 최대 상승 (0) | 2025.09.06 |
| [Baekjoon/C++] 2896번 - 무알콜 칵테일 (0) | 2025.08.29 |
| [Baekjoon/C++] 28062번 - 준석이의 사탕 사기 (1) | 2025.08.26 |
